From the Q&A

With TJ Byers

Isaac Newton, Calculus, And Op Amps

Question:

I always thought it was interesting that you could perform differentiation and integration using an op amp. Could you show how to make both circuits accurately with a CA5160 or an LM358 op amp? I would like to interface the circuits to my microprocessor, then view the I/O results on the 'scope.

Keith Penner
via Internet

Answer:

During WWII, derivative and integral functions using analog amplifiers were a critical part of the war effort. These analog computers were used to pinpoint artillery targets, map bombing raids, and sat at the very heart of the newly-invented RADAR. Described independently by Wilhelm Liebniz and Issac Newton in the 17th century, they were just a mathematical curiosity and mental exercise — until Newton recognized (in 1665) that the two are actually mirror images of each other (inverse functions) and could be applied to practical physics problems. As the physical world expanded from cannonballs to electrons, so did the applications for these two mathematical functions.

Here are two simple differentiator and integrator circuits that can be used to show what happens when a signal is processed by each.

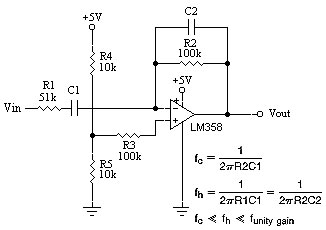
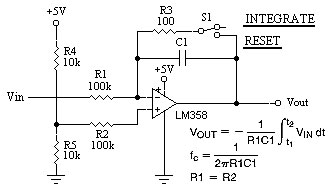
The differentiator works in real time, whereas the integrator takes a snapshot of an event and has to be reset by shorting out the capacitor. The resistance values shown are just ballpark values to bias the op amp into a linear region, and can be changed to match your frequency needs — just be careful that you don't set the gain too low (below unity) or too high (typically above 100). The equations are shown on the schematics.