Pinochle is an American card game typically played by three players acting alone (cutthroat) or four players in two partnerships. The game probably derives from a German variety of bezique.
I belong to a group who enthusiastically plays Pinochle once a week. Unfortunately, with the present circumstance of social distancing during the COVID-19 pandemic, we have been deprived of our weekly get together. So, with today’s technology and an introduction to the virtual conferencing provided by Zoom, I decided to see if we could play Pinochle online. Here’s what I came up with.
Four-handed Pinochle requires cards from four decks, using only the 10s, Jacks, Queens, Kings, and Aces. First thing therefore was to obtain 16 decks of cards and prepare four Pinochle decks — one for each of the team.
The plan was to set up a meeting online using Zoom, so that we four could see and speak with each other. Next, we needed to be able to deal four hands of 20 cards each to simulate the conventional shuffle, cut, and deal process that we’re used to.
Having cards in our hands, the game could proceed with the bidding, melding, scoring, and playing as per usual, relying on good faith of course, but since there was no financial aspect to our game, that wasn’t a problem.
I needed a program which would deal four random hands and produce files that could be distributed to the players via email. Each player could then translate the file data into real cards from their own decks of cards. The challenge was to find or write a program to fit the bill.
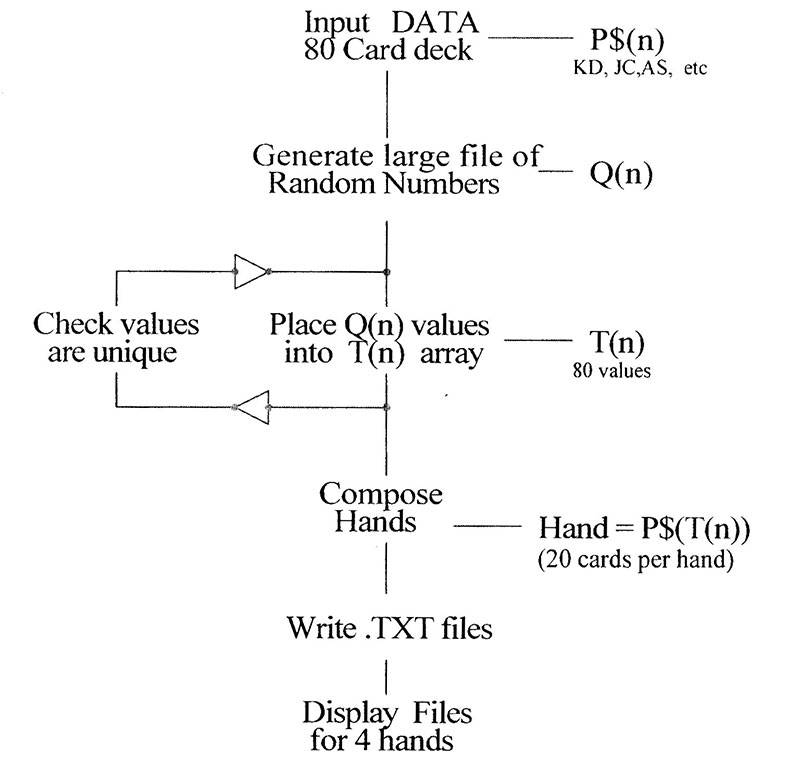
Program flowchart.
Good old Basic from 35 years ago to the rescue! Another trip down memory lane! I found that PC-BASIC is a free online software that will run Basic programs on a Windows 10 computer since the old standby GW-Basic fell off the scene after Windows XP disappeared.
I know that purists and professional programmers have long said goodbye to the Basic language, but that was all we had in the early ‘80s and it does the job.
The program listed here worked very well. It was a bit slow because I was generating 1,000 random numbers each time. Experimenting with the size of the pool of random numbers it seeded, I thought I might get away with 300. But just to be safe, I left the number at 1,000.
Having finished, tested, and used the program, I went on to modify it to produce the three hands needed for the cutthroat Pinochle version. It’s different because a single three card box is needed to go with the three hands, each of 15 cards only.
So, all the numbers needed changing. While I was at it, I wrote a third version of the program that gives four hands of 13 cards that could be used to organize a round of Bridge, perhaps.
Having run the program 10 times using different seeds to trigger the Randomize function to produce the hands for 10 games, all that remained was to collect the ASCII files that were saved as .TXT and collate the data to email to all the players.
To run the Basic program, it’s necessary to run PC_BASIC first, and then run the Cards.Bas program on that platform. The two programs — CARDS and 3HAND — are included here and with the article downloads. NV
10 ‘PROGRAM IS CARDS
20 ‘P$(n) is Pinochle Deck
30 CLS : SIZ = 1000 : DIM P$(80): DIM Q(SIZ) : DIM T(100)
40 DIM NORTH$(20) : DIM SOUTH$(20) : DIM EAST$(20) : DIM WEST$(20)
50 DATA 10H,JH,QH,KH,AH,10C,JC,QC,KC,AC,10D,JD,QD,KD,AD,10S,JS,QS,KS,AS:
60 FOR N=1 TO 20 : READ P$(N) : NEXT N ‘Load 20 card deck and copy 3 times
70 FOR N=1 TO 20 : P$(N+20)=P$(N) : P$(N+40)=P$(N) : P$(N+60)=P$(N) : NEXT N
80 ‘
90 ‘ FILL Q(n) ARRAY WITH RANDOM NUMBERS FROM 1 TO 80
100 PRINT “Enter Randomize seed “; : INPUT R$ : PRINT ,,” working”
110 R = VAL(R$) : RANDOMIZE (R)
120 FOR I=1 TO SIZ
130 X = FIX(RND*90) : IF X<1 OR X>80 THEN 130
140 Q(I)= X : NEXT I
150 ‘
160 ‘ SELECT NUMBERS TO FILL T(n)
170 F = 1 : FOR A = 1 TO SIZ ‘Pick data 1 to 80
180 FOR B = 1 TO 80 ‘Compare with T array
190 IF Q(A) =T(B) THEN 220
200 NEXT B
210 T(F) = Q(A) : F = F+1 : IF F = 81 THEN 230 ‘go till T(n) is full
220 NEXT A
230 FOR M = 1 TO 80 : PRINT T(M); : NEXT M
240 ‘
250 ‘ WRITE TEXT FILES & DISPLAY DATA
260 FOR N = 1 TO 20 : NORTH$(N) = P$(T(N)) : NEXT N
270 FL$=”North “+R$+”.TXT” : OPEN “O”,1,FL$
280 PRINT#1,R$;” “; : FOR N = 1 TO 20 : PRINT#1,NORTH$(N);” “; : NEXT N
290 CLOSE #1
300 FOR N = 21 TO 40 : SOUTH$(N 20) = P$(T(N)) : NEXT N
310 FL$=”South “+R$+”.TXT” : OPEN “O”,1,FL$
320 PRINT#1,R$;” “; : FOR N=1 TO 20 : PRINT#1,SOUTH$(N);” “; : NEXT N
330 CLOSE #1
340 FOR N = 41 TO 60 : EAST$(N 40) = P$(T(N)) : NEXT N
350 FL$=”East “+R$+”.TXT” : OPEN “O”,1,FL$
360 PRINT#1,R$;” “; : FOR N = 1 TO 20 : PRINT#1,EAST$(N);” “; : NEXT N
370 CLOSE #1
380 FOR N = 61 TO 80 : WEST$(N 60) = P$(T(N)) : NEXT N
390 FL$=”West “+R$+”.TXT” : OPEN “O”,1,FL$
400 PRINT#1,R$;” “; : FOR N = 1 TO 20 : PRINT#1,WEST$(N);” “; : NEXT N
410 CLOSE #1
420 ‘
430 CLS : PRINT : PRINT : PRINT , “Hands dealt for game #”;R : PRINT
440 PRINT “North “; : FOR N=1 TO 20 : PRINT NORTH$(N);” “; : NEXT N : PRINT
450 PRINT “South “; : FOR N=1 TO 20 : PRINT SOUTH$(N);” “; : NEXT N : PRINT
460 PRINT “East “; : FOR N=1 TO 20 : PRINT EAST$(N);” “; : NEXT N : PRINT
470 PRINT “West “; : FOR N=1 TO 20 : PRINT WEST$(N);” “; : NEXT N : PRINT
480 PRINT “ “ : PRINT ,”**********************************************”
490 END
CARDS program.
10 ‘PROGRAM IS 3HAND
20 CLS : SIZ=1000 ‘P$(n) is 3 hand deck
30 DIM P$(48): DIM Q(SIZ) : DIM T(100) ‘Q(n) are random numbers
40 DIM PLAY1$(20) : DIM PLAY2$(20) : DIM PLAY3$(20)
50 DATA 9H,10H,JH,QH,KH,AH,9C,10C,JC,QC,KC,AC : ‘Single deck
60 DATA 9D,10D,JD,QD,KD,AD,9S,10S,JS,QS,KS,AS
70 FOR N=1 TO 24 : READ P$(N) : NEXT N ‘Load 24 card deck
80 FOR N=1 TO 24: P$(N+24)=P$(N) : NEXT N ‘twice
90 ‘
100 ‘ FILL Q(n) ARRAY WITH RANDOM NUMBERS FROM 1 TO 48
110 PRINT “Enter Randomize seed “; : INPUT R$ : PRINT ,,” working”
120 R = VAL(R$) : RANDOMIZE (R)
130 FOR I=1 TO SIZ
140 X = FIX(RND*50) : IF X<1 OR X>48 THEN 140
150 Q(I)= X : NEXT I
160 ‘
170 ‘ SELECT NUMBERS TO FILL T(n)
180 F=1 : FOR A = 1 TO SIZ ‘Pick data (1 to 48)
190 FOR B = 1 TO 48 ‘Compare with T array
200 IF Q(A) = T(B) THEN 230 ‘If present try again
210 NEXT B
220 T(F) = Q(A) : F = F+1 : IF F = 49 THEN 240 ‘go till T(n) is full
230 NEXT A
240 FOR M = 1 TO 48 : PRINT T(M); : NEXT M
250 ‘
260 ‘ WRITE (.TXT) FILES & DISPLAY DATA
270 FOR N = 1 TO 15 : PLAY1$(N) = P$(T(N)) : NEXT N
280 FL$=”Play1 “+R$+”.TXT” : OPEN “O”,1,FL$
290 PRINT#1,R$;” “; : FOR N = 1 TO 15 : PRINT#1,PLAY1$(N);” “; : NEXT N
300 CLOSE #1
310 FOR N = 16 TO 30 : PLAY2$(N 15) = P$(T(N)) : NEXT N
320 FL$=”Play2 “+R$+”.TXT” : OPEN “O”,1,FL$
330 PRINT#1,R$;” “; : FOR N=1 TO 15 : PRINT#1,PLAY2$(N);” “; : NEXT N
340 CLOSE #1
350 FOR N = 31 TO 45 : PLAY3$(N 30) = P$(T(N)) : NEXT N
360 FL$=”Play3 “+R$+”.TXT” : OPEN “O”,1,FL$
370 PRINT#1,R$;” “; : FOR N = 1 TO 15 : PRINT#1,PLAY3$(N);” “; : NEXT N
380 CLOSE #1
390 FOR N = 46 TO 48 : BOX$(N 45) = P$(T(N)) : NEXT N
400 FL$=”Box “+R$+”.TXT” : OPEN “O”,1,FL$
410 PRINT#1,R$;” “; : FOR N = 1 TO 3 : PRINT#1,BOX$(N);” “; : NEXT N
420 CLOSE #1
430 ‘
440 CLS : PRINT : PRINT : PRINT , “Hands dealt for game #”; R : PRINT
450 PRINT “Player1 “; : FOR N=1 TO 15 😛RINT PLAY1$(N);” “; :NEXT N : PRINT,,””
460 PRINT “Player2 “; : FOR N=1 TO 15 😛RINT PLAY2$(N);” “; :NEXT N : PRINT,,””
470 PRINT “Player3 “; : FOR N=1 TO 15 😛RINT PLAY3$(N);” “; :NEXT N : PRINT,,””
480 PRINT “Box”; R; : PRINT “ “;: FOR N=1 TO 3 : PRINT BOX$(N);” “; : NEXT N
490 PRINT ,,,,”” : PRINT ,”***************************************”
500 END
3HAND program.
Downloads
What’s in the zip?
CARDS Program
3HAND Program


