1/f Random Tones — Making Fractal Music with an Arduino

» Skip to the Extras

Back in 1973, I was looking at a wall. The writing on it said to learn about computers. So, I took a course in computer repair and never looked back.

My wife bought me a KIM-1 single board computer for my birthday in 1976; it cost $245. I wrote a KIM-1 program in assembly language that played 1/f random notes. I wrote an article about it, and in July 1976 it was published in Personal Computing called, “1/f Random Tones.” They paid me $400. It paid for the computer for sure.

During the rest of the ‘70s, I wrote a lot of programs for it and began writing articles about the programs. The KIM-1 had 1K of RAM and 2K of ROM. It stored programs on cassette tape, had a six-character display, and you had to program it in assembly language using hex numbers with an ASCII keypad for entry.

After a couple years, I bought boards to make the KIM-1 a little smarter which allowed me to program in BASIC; that would have been “Microsoft Cassette BASIC.” I was having a problem with it and called Microsoft. I actually got to talk to Bill Gates on the phone at the time. What did he have to say: “Call your vendor.”

I eventually updated my computer life by getting a Tandy/RadioShack TRS-80. I built an IBM Selectric Terminal printer interface and printer driver that was published in a British magazine called Wireless World.

The Selectric had solenoids in it to drive all the keys. Thus, I was able to print all my code and other writings out in letter quality print. It was slow, but beautiful. There were many, many computer magazines on the store racks at the time and I wrote articles for many of them. Back in 1980, Nuts & Volts was printed on newsprint and actually looked like a newspaper.

Since we don’t have to use ancient computers any more in our programming, I decided to write the 1/f program using an Arduino. However, let’s first talk a bit about 1/f music.

For a long time, fine arts have been duplicating nature, or at least trying to imitate her as much as possible. Yet, music seems to be the least imitative of those arts. So, how can it be connected to nature’s seemingly structured randomness? Well, a certain statistical property of the world appears to be the connection. This property was discovered by Richard F. Voss, an IBM physicist. His discovery concerns the relation or “autocorrelation” between vibrations and their power spectrum.

To understand this concept, we have to consider types of random sounds. For instance, changing the speed at which you play music on your old phonograph naturally decreases or increases the sound’s pitch. However, a type of sound called “scaling noise” sounds the same no matter what speed you play it at. An example is white noise like the random noise produced in a resistor, or even plain static. One bit of noise is completely unrelated to the last bit or any future bit. Its autocorrelation factor is zero. You can write a program to generate such random notes, but it soon becomes boring.

A more correlated noise called Brownian noise is also random, but each bit of noise is related to the last bit and to the next bit. To get a picture of this type of noise, imagine a butterfly flying. Its path is apparently random, yet it is connected, though in a wandering flight. Although music made from Brownian noise has a high autocorrelation factor, it still tends to be dull.

Halfway between white and Brownian noise is Voss’ discovery, or 1/f noise. If white noise is 1/f⁰ and Brownian noise is 1/f², halfway is naturally 1/f, or pretty close to it. Basing music on this type of noise is a lot more fun and interesting.

Before I get to that, I should explain the term “fractals.” Benoit B. Mandelbrot coined the term to cover a class of patterns having the property that no matter how closely you look at them, they always look the same. He discovered that the flooding of the Nile, variations in sunspots, and undersea currents are based on 1/f fluctuations. Voss said our total experience is based on 1/f noise.

An article by Martin Gardner in Scientific American (April 1978) contained an example showing how to produce 1/f numbers using dice. I took that example and programmed the KIM-1 to do it repeatedly, and to play notes and tunes based on the 1/f numbers. This time, I used an Arduino.

How the Program Works

Say we get three dice, or rather program our computer to get them. We also make three columns of binary numbers with each column representing one of the dice. Since there are three dice, we need to count in binary up to 2³, or eight. Refer to Figure 1.

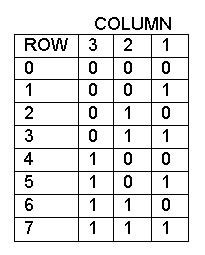
FIGURE 1. Column change table.

To determine what row is to be thrown, we have a sequence of eight numbers (3, 1, 2, 1, 3, 1, 2, 1) stored in an array called NumColsToChangeN. Since the first number is 3, we throw all three dice. The three dice (actually generated random numbers) are added up; this sum points to a note on a piano or, in our case, to a note in memory in another array.

The second number in the NumColsToChangeN array is 1, so we throw one dice in the one column. After we throw the one dice, all three dice are added up again, and we point to another note. The next number is 2, so two dice are thrown and again all three are added.

This process continues until we have a pattern for the eight rows. After row seven, the whole thing repeats. The numbers generated are random, yet (as you can see) the dice in column three changes occasionally, in column two more so, and all the time in column one.

Thus, we create 1/f random numbers. These random numbers are very closely correlated due to the always changing one’s column, and the least changing two and three columns. Take a look at the flowchart in Figure 2.

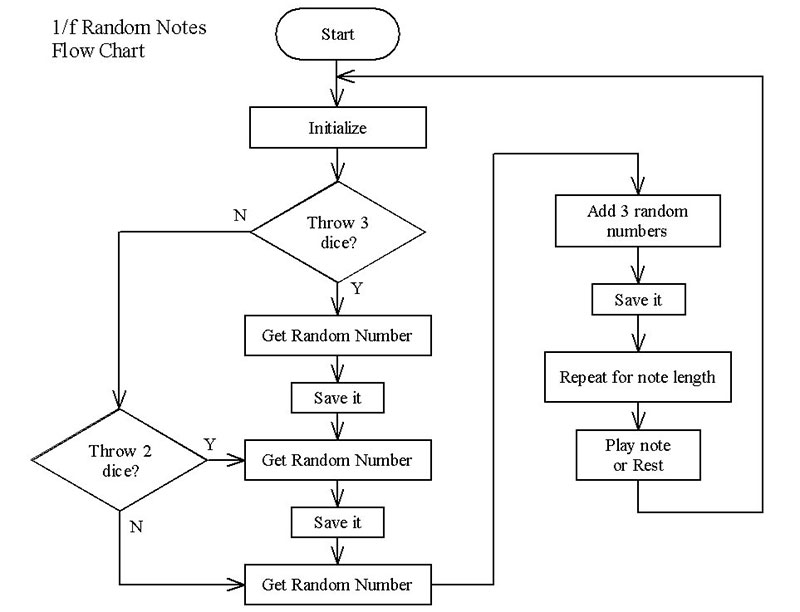
FIGURE 2. Program flow chart.

About the Arduino Program

I’ve put in a lot of comments in the code (available in the downloads), so it should be fairly easy to follow what I did.

However, let’s go to the program to see how it does all this. Load the Arduino sketch One_Over_F_Random_ Numbers.ino or view the One_Over_F_Random_ Numbers.txt file in the downloads.

As in all Arduino programs, we have various sections. The first section in this one describes the circuit diagram. The Arduino circuit diagram can be seen in Figure 3.

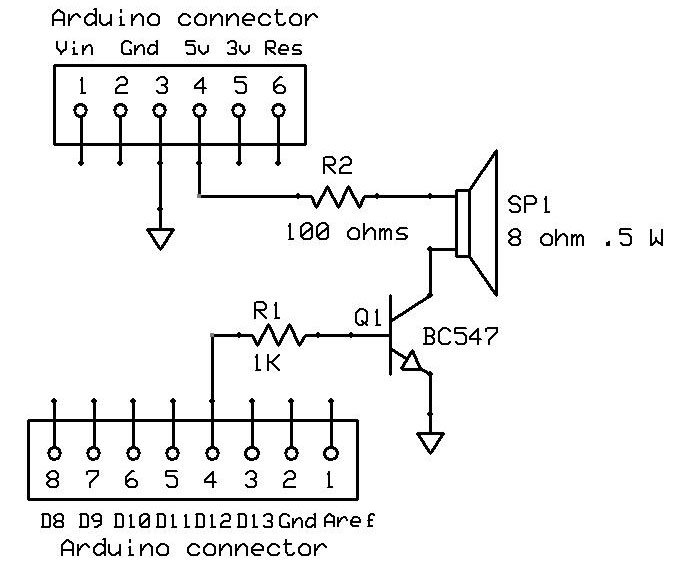
FIGURE 3. Arduino schematic.

I chose an Arduino Uno, but almost any Arduino can be used. By changing the resistor in the speaker circuit (R2), the volume can be changed a bit (Figure 4).

FIGURE 4. Arduino circuit.

All the notes are listed in the note_table.h file. It’s added to the Arduino program by clicking Sketch, Add File. The note values can then be compiled into the program by the #include “note_table.h” line. If you look at the note table, the notes are labeled like NA1 for example. The N was added because A1 is an Arduino word representing the analog pin 1 and will produce a syntax error. All notes, therefore, are prepended with an N.

The next section sets up the variables in the program. In order to determine the lengths of notes, we have to decide on what tempo we want the notes to play at. The tempo is one minute divided by a number; in this case, 120 beats per minute. This gives us the length of a quarter note (Q in the program). From there, we can use simple math to determine the lengths of the other common notes: sixteenth (S), eighth (E), and whole (W). If you want to play things slower or faster, this is the number to change.

We are generating a lot of random numbers, so they are put into variables Rnd0 to Rnd7. I know that we can avoid a lot of the variables through smart programming, but I have a tendency to keep things understandable. After all, I’ve been programming a long time, and the variables in my 72 year old brain are slowly disappearing, so keep it simple; we have a lot of young brains to teach.

Next, we come to the notes in a sequence section. In this section are a bunch of notes that we can use to play with. First, we have notes from C₃ to A₄ which is about midrange on a piano:

int sequence[] = {1,1,1, NC3,ND3,NE3,NF3,NG3,NA3,NB3,NC4, ND4,NE4,NF4,NG4,NA4, 1,1,1};

This is the sequence we use first. It allows you to hear what 1/f music is like. Then, you can try different scales or create different note sequences for yourself.

The sequence is an array. The three 1s at the beginning are there because when we add up three dice with ones being thrown, we come up with the number 3. When you access an array, it always starts at 0, so we have to start our notes at the fourth position, or 3. The 1s at the end are for rests or no notes played. 1/f notes will have a tendency to hang around the middle of the sequence, so rests aren’t often played; after all, you don’t want to hear too many nothings.

As you go on with trying out other sequences, comment the first sequence and then uncomment the sequence you want to try. For instance, notes in the pentatonic scale are oriental in nature.

If you want to go farther in trying out different programming techniques — such as making the array smaller — then put the size of the array in the random function. We can determine the length of the sequence array, lenSeq, by using the Arduino function sizeof(). Sizeof returns the number of bytes in the array. Be careful of this length, however. It could be counting more than just the data in the array. Test this very carefully.

The length of the notes — or note durations — is found in another array: noteDurations. Since we are 1/f randomizing the durations, we are only using two dice instead of three. The beginning will therefore start at 2 in the array.

The standard Arduino setup section is next. We make sure the pin the speaker is on is set as an output, and we set the serial port so we can see the note values (and other values) if we need to.

Next, we set a random seed from an unset analog pin. Check out the Arduino reference on this online if you need to see why we do this. Basically, it’s to make sure the random numbers created are as random as possible.

Finally, we get to the main loop of the program. We use a counter to create the random numbers from 0 to 7 from the NumColsToChangeN array. Remember, its numbers are 3, 1, 2, 1, 3, 1, 2, 1:

// Play 8 random notes for (i=0; i<8; i++) { Row = NumColsToChangeN[i]; switch (Row){ case 3: // Throw 3 dice Rnd1 = random(1, 7); // 1 to 6 dots Rnd2 = random(1, 7); Rnd3 = random(1, 7); case 2: // Throw 2 dice Rnd1 = random(1, 7); Rnd2 = random(1, 7); case 1: // Throw 1 di Rnd1 = random(1, 7); } Rnd0 = Rnd1 + Rnd2 + Rnd3; // Min 3 (1+1+1), Max 18 (6+6+6)

So, the first number will be 3, and we get three random numbers. The random(min, max) function has a silly way of creating numbers. Min is inclusive and max is exclusive; this means if you want four random numbers, min will designate the lowest number (say, 1) and max must be 5. Maybe someday this will be fixed.

The first time through the loop we are throwing three dice. We get a random number from one to six that represents the dots on a dice. Next, we get the second and third random numbers. We add them up, and the sum gets stored in Rnd0. Then, we get the note length in a similar manner and that gets stored in Rnd6. Finally, we get just a regular random rest length:

// Get a rest length Rnd7 = random(0, 3); // Get a random # from 0 to 2 (S,E,Q) rest = restDurations[Rnd7];

This could be 1/f generated if you want to do that, as well. The actual rest length (in milliseconds) comes from the restDurations array, but we are only looking for a sixteenth, eighth, or quarter note in this program. You can add in more notes if you want. The note duration is pulled from the noteDurations array, and the note frequency is pulled from the sequence array:

// Play the note or rest duration = noteDurations[Rnd6]; freq = sequence[Rnd0]; // This plays a rest if (freq == 1) { playRest(duration,rest); } if (freq > 1) { playTone(duration,freq); } //ShowIt(); // For testing

If the frequency is a 1, we play the rest with the playRest function. If the frequency is more than a 1, we play the note with the playTone function. Finally, if we want to see any variable, we run the ShowIt function.

I pulled the playTone function off the Internet (thanks to those who wrote it); basically, you provide the duration (duration) and the frequency (freq) to it, and it pulses the speaker pin. The playRest function doesn’t pulse anything; it just provides empty time.

After eight notes, we start the whole thing over again. You can throw in delays in the loop and the ShowIt function to slow things down a bit, which is probably needed when you want to see the variables in the serial monitor on the screen. You can also make the length as long as you want by changing the index.

So, that’s that. Play the different sequences and see how they sound. Do they actually sound like something resembling music? I think they are more musical than just plain random numbers. Even my musical professional wife thought so.

There are MP3 files included in the downloads for you to listen to. One is a sequence from the middle notes of a piano; the next one is a sequence from a Pentatonic scale which (as mentioned previously) is oriental in nature; and the third one is a sequence from the notes in the movie, Close Encounters of the Third Kind.

Go to www.scientificamerican.com/magazine/sa and buy the magazine (April 1978, Vol 238, Issue 4). The 1/f random numbers article is in Martin Gardner’s Mathematical Games section titled, “White and brown music, fractal curves, and one-over-f fluctuations.”

Maybe there’s a better program that can be created to make better computer music. Are you one of those who can write it? NV

For the random tones, it really only requires four parts: