Smiley’s Workshop 5: There are 10 types of people. Those who get binary and those who don’t.

Figure 1. Ten types of people.

Smiley's Workshop — AVR C Programming Workshop Series - Part 5

Last episode, we learned some more C syntax, a bit about libraries, and taught our Butterfly to talk. This time, we are going to learn what the heck that button in Figure 1 means. If this doesn’t make sense to you now, it will in a minute (or two).

Bitwise Operator

Table 1: Bitwise Operators
Operator	Name	Example	Defined
~	Bitwise complement NOT	~x	Changes 1 bits to 0 and 0 bits to 1
&	Bitwise AND	x&y	Bitwise AND of x and y
\|	Bitwise OR	x\|y	Bitwise OR of x and y
^	Bitwise exclusive OR	x^y	Bitwise XOR of x and y
<<	Left shift	x<<2	Bits in x shifted left 2 bit positions
>>	Right shift	x>>3	Bits in x shifted right 3 bit positio

Bitwise operators are critically important in microcontroller software. They allow us to do many things in C that can be directly and efficiently translated into microcontroller machine operations. This is a dense topic, so get out a pencil and piece of paper and work through each of the examples until you understand it.

In case you’ve ever wondered how to tell what is true and what is false — well for bitwise operators which use binary logic (single bits) — 1 is true and 0 is false.

We discussed binary vs. hexadecimal vs. decimal in Workshop 3, but to refresh: A byte has 256 states numbered 0 to 255. We number the bits in a byte from the right to the left as lowest to highest:

bit # 76543210 myByte = 01010101 binary = 0x55 hexadecimal = 85 decimal

Look at the truth tables for AND ‘&’, OR ‘|’, XOR ‘^,’ and NOT ‘~:’

AND OR XOR NOT 0 & 0 = 0 0 | 0 = 0 0 ^ 0 = 0 ~1 = 0 0 & 1 = 0 0 | 1 = 1 0 ^ 1 = 1 ~0 = 1 1 & 0 = 0 1 | 0 = 1 1 ^ 0 = 1 1 & 1 = 1 1 | 1 = 1 1 ^ 1 = 0

Now memorize them. Ouch, but yes, I am serious.

ORing

We can set bit 3 to 1 in a variable, myByte, by using the Bitwise OR operator: ‘|’

myByte = 0; myByte = myByte | 0x08;

To see what’s happening, look at these in binary:

bit # 76543210 myByte = 00000000 = 0x00 0x08 = 00001000 = 0x08 ———————————————————————— OR = 00001000 = 0x08

We see that bit 3 is 1 in 0x08 and 1 | 0 = 1, so we set bit 3 in myByte.

Suppose myByte = 0xF7:
bit # 76543210 myByte = 11110111 = 0xF7 0x08 = 00001000 = 0x08 ———————————————————————— OR = 11111111 = 0xFF

Or maybe myByte = 0x55:

bit # 76543210 myByte = 01010101 = 0x55 0x08 = 00001000 = 0x08 ———————————————————————— OR = 01011101 = 0x5D

This shows that only bit # 3 of myByte is changed by the OR operation. It is the only bit equal to 1 in 0x08, and ORing 1 with anything else is always yields 1, so you can use it to ‘set’ a bit regardless of that bit value.

ANDing

Now let’s do the same thing with the & operator:
We can clear bit 3 with:

myByte = 0xAA; myByte = myByte & 0xF7;

bit # 76543210 myByte = 10101010 = 0xAA 0xF7 = 11110111 = 0xF7 ———————————————————————— AND = 10100010 = 0xA2

Or maybe myByte = 0x55:

bit # 76543210 myByte = 01010101 = 0x55 0xF7 = 11110111 = 0xF7 ———————————————————————— AND = 01010101 = 0x55

From this, you see that ANDing with 1 leaves the bit value the same as the original bit and ANDing with 0 clears that bit regardless of its state. So, you can use ANDing with 0 to ‘clear’ a bit value.

Setting and clearing bits is very important in AVR microcontrollers since the plethora of peripherals available are set up by either setting or clearing the hundreds of bits in dozens of byte-sized registers.

Setting and Clearing Bits

In each of the above cases, we are only dealing with a single bit, but we might be interested in any or all of the bits. Another important feature of using bitwise operators is that it allows us to set or clear a specific bit or group of bits in a byte without knowing the state of nor affecting the bits we aren’t interested in. For example, suppose we are only interested in bits 0, 2, and 6. Let’s set bit 6, regardless of its present value, then clear bits 0 and 2, also regardless of their present value. Here’s the trick: We must leave bits 1, 2, 4, 5, and 7 as they were when we began.

NOTE:
myByte = myByte | 0x08;
is the same as
myByte |= 0x08;
which we will use from now on. To set bit 6, we OR myByte with 0100000 (0x40):

myByte = 42; myByte |= 0x40;

bit # 76543210 myByte = 00101010 = 0x2A 01000000 = 0x40 ———————————————————————— OR = 01101010 = 0x6A

Next, we want to clear bits 0 and 2 so we AND 11111010:

myByte &= 0xFA;

bit # 76543210 myByte = 01101011 = 0x6B 0xFA = 11111010 = 0xFA ———————————————————————— AND = 01101010 = 0x6A

So, in summary, we set bits with ‘|’ and clear bits with ‘&.’

If you are going ‘Oh my God!’ at this point, I hope it is because you are surprised that you actually understand this. If it isn’t, then get that pencil and paper and go back until you do.

XORing

Suppose we want to flip the highest four bits in a byte while leaving the lowest four alone; we could use a mask with the bits you want to flip set to 1 and the bits you don’t want to flip set to 0:

myByte = 0xAA; myMask = 0xF0;

myByte ^= myMask;

bit # 76543210 myByte = 10101010 = 0xAA myMask = 11110000 = 0xF0 ———————————————————————— XOR = 01011010 = 0x5A

XORing is used a lot by cryptographers, but not a lot by us mortals.

NOTing

Using the above example, we could clear those bits in myByte using the NOT on the mask, then AND it with myByte.

myByte = 0xAA; myMask = 0xF0;

myMask = 11110000 = 0xF0 ~myMask = 00001111 = 0x0F

myByte &= ~myMask;

bit # 76543210 myByte = 10101010 = 0xAA ~myMask = 00001111 = 0x0F ———————————————————————— AND = 00001010 = 0x0A

Shift Operators

The shift operators can be used to radically speed up multiplication and division IF you use numbers that are a power of 2. You might want to do this for tasks like averaging ADC readings. When we study ADC, you’ll see that sometimes we can get more accurate results if we take a bunch of readings and average them. My first inclination was to take 10 readings and then divide by 10. I chose 10 because I’ve got that many fingers, but if I had chosen eight or 16, then my division would be much faster on a binary computer using >>. If I divide by 10, the compiler has to call a large and complex division function (and maybe even involve floating-point data types) but if I divide by eight it only needs to shift bits three positions to the right. Three quick right shift operations versus lots of time and program space – the trade-off is precision.

Let’s say my readings were:

54, 62, 59, 57, 60, 59, 56, 63 = 470

The sum is 470 and 470 / 8 = 58.75

Remember that the largest decimal number that fits in an eight-bit byte is 256, so we must store 470 in a 16-bit integer: 0000000111010110.

myTotal = 470

bit # FEDCBA9876543210 (in Hex) myTotal 0000000111010110

If we shift this right three times, it becomes:

myAverage = (myTotal >> 3);

bit # FEDCBA9876543210 >> 3 0000000000111010110

The low three bits 110 fall out of the AVR and have to be swept up later. (You didn’t believe that did you? They actually just disappear.) Anyway, the value now (ignoring the leading zeros) is 111010 which is decimal 58.

Note that 58 is not 58.75, but you did save both time and program space, so you have to decide which is better to use. The binary averaging gets you closer than all but two of the eight readings (59) and it does it lightning fast so if you are time constrained, the trade-off should be obvious.

Masks and Macros: Using Named Bits

You probably didn’t know this, but Cylon eyes don’t just sweep a single LED back and forth at one speed. No, when they get excited the sweep speeds up and if they get really excited they sweep more LEDs. When they are feeling contrary, they can invert the pattern. When they get walloped up side the head, they do this weird walleye sweep. When they get really mad, the LEDs vibrate. When they get confused, they do an ant sweep. When they see an actual chrome toaster — like with bread in it — they blink all LEDs on and off. And when they get infected with Microsoft Windows, they generate random dots until reset. Finally, the sweep has 16 speeds.

We have seven patterns and we can encode them with three switches as follows:

Binary Decimal Pattern Select 000 0 cylonEyes 001 1 cylonEyes2 010 2 cylonEyes3 011 3 wallEyes 100 4 antEyes 101 5 vibroEyes 110 6 blinkinEyes 111 7 randomEyes

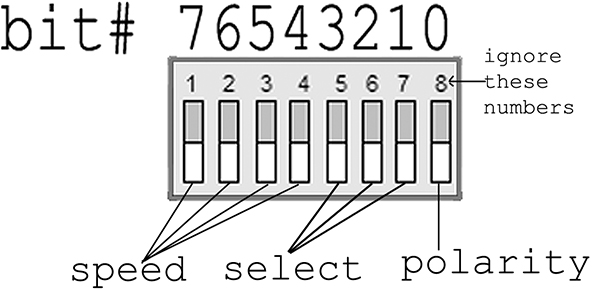Figure 2. DIP switch use.

If you want to get your Cylon Optometry Doctorate, you have to figure out how to encode those seven patterns, the 16 speeds, and the polarity using just eight switches. We will use bitwise operators, masks, and macros to do just that for our CylonOptometry.c project. So, dig out that PortI/O hardware project and reverse the wires so that DIP switch 8 goes to PORTB 0, 7 to 1, 6 to 2, and so on. Yes, sorry, but I want the switches to match the bits in a binary number like: bit #76543210 with the rightmost switch being bit 0 and the leftmost being bit 7. Figure 2 shows the switch pattern.

Now we will define bit masks:

// DIP switch masks #define POLARITYMASK 0x01 // 00000001 #define SELECTMASK 0x0E // 00001110 #define SPEEDMASK 0xF0 // 11110000

If we AND each of these masks with the value we read on PORTB, we convert all the bits we aren’t interested in to 0 and leave those we are interested in as they were in the port.

Suppose, for instance, that we set the speed to 9, the pattern select to 6, and the polarity to 1. We would see 10011011 (0x9B).

PORTB = 10011011 (0x9B)

bit # 76543210 PORTB = 10011011 = 0x9B POLARITYMASK = 00000001 = 0x01 ——————————————————————— AND = 00000001 = 0x01

bit # 76543210 PORTB = 10011011 = 0x9B SELECTMASK = 00001110 = 0x0E ——————————————————————— AND = 00001010 = 0x0A

bit # 76543210 PORTB = 10011011 = 0x9B SPEEDMASK = 11110000 = 0x01 ——————————————————————— AND = 10010000 = 0x90

We have isolated the bit fields for each mask, but we still have one more step. You will note that the polarity can be only 0 or 1 — which is fine — but the pattern select does not directly indicate the number of the pattern since it begins at the second bit, not the first. So each value is multiplied by two. Our count is not 0,1,2,3,4,5,6,7; it is 0,2,4,6,8,10,12,14. We could use this numeric sequence to define our pattern states, but it would be much simpler if we could just shift the whole byte one position to the right, dropping the first bit into the void – and we can do that with the right shift operator >>. Our mask gave us: 00001010 = 0x0A. But (00001010 >> 1) is equal to 00000101 or for hex 0x0A >> 1 equals 0x06. The same idea holds true for the speed value that we right shift 4: (0x90 >> 4) is equal 0x09.

In CylonOptometry.c, we read the switch state, mask off the polarity, speed, and pattern, shift them, and then use a switch statement to select the function for the specified pattern. Each of these seven functions runs through an array containing the pattern to show on the LED and calls the dillydally() function that delays a number of milliseconds depending on the speed setting. It then checks to see if PORTB has changed. If not, it returns 0 to the function that will show the next pattern in the array. If PORTB has changed, then it returns 1 and the function will return to main(), and run the switch statement again to see if a new pattern has been selected.

The following is from the cylonEyes section of the program:
/* 00000001 == 0x01 00000010 == 0x02 00000100 == 0x04 00001000 == 0x08 00010000 == 0x10 00100000 == 0x20 01000000 == 0x40 10000000 == 0x80 01000000 == 0x40 00100000 == 0x20 00010000 == 0x10 00001000 == 0x08 00000100 == 0x04 00000010 == 0x02 */ void cylonEyes() { uint8_t i = 0; uint8_t ce[] = { 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80 };

while(1) { // run up the array for(i = 0; i <= 7; i++) { if(dillyDally()) return; // delay or bail if(Polarity) PORTD = ce[i]; // show non-invert
else PORTD = ~ce[i]; // show inverted } // run down the array for(i = 6; i >= 1; i—) { if(dillyDally()) return; // delay or bail if(Polarity) PORTD = ce[i]; // show non-invert else PORTD = ~ce[i]; // show inverted } } }

Whoa, we were having so much fun that we’ve run ourselves plum out of space. By now, you should know that Figure 1 means binary 10 people is decimal 2 people. The rest of the CylonOptometry software and a text supplement is in CylonOptometry.zip that you can get at the downloads link below or at www.smileymicros.com.

A note for Vista users and those folks who want to use the most recent WinAVR and AVRStudio: You can download from www.smileymicros.com ‘New Quick Start Guide’ and ‘C Projects Source Code for Vista.’ NV

Joe Pardue has a BSEE and operates www.smileymicros.com from the shadows of the Great Smokey Mountains in Tennessee. He is author of Virtual Serial Port Cookbook and C Programming for Microcontrollers

WORKSHOP BOOKS & KITS

If you’re following this series and want to read further or jump in and try the experiments, click this banner to go to the Nuts & Volts webstore where you’ll find all the hardware kits being used throughout, as well as Joe’s books. It’s a great way to learn microcontroller programming with C and get the kind of hands on experience, as you go, that brings the lessons to life.