With TJ Byers
Lissajous Reflections
Question:
I remember making interesting Lissajous figures in a physics class years ago. Could you explain their uses and how to make them on an oscilloscope?
Keith Penner
via Internet
Answer:
A Lissajous pattern is a graph of a curve in which both the x and y Cartesian coordinates are periodic functions of time (t) given by equations — typically, x = sin(nt + c) and y = sin(t). Different patterns may be generated for different values of n and c. A Lissajous figure is easily generated on the screen of an oscilloscope by turning off the internal horizontal sweep and applying a sinewave to both the vertical and external horizontal inputs. The shape of the pattern is a function of the frequency ratio and phase angle between the two signals. For example, if the two sine waves are in phase and of the same frequency, the screen displays a circle. A frequency ratio of 2:1 generates a figure eight pattern and a ratio of 3:1 produces three loops, like the one shown below.
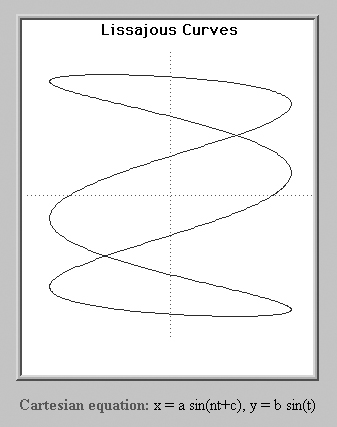
Before electronic counters, Lissajous patterns were often used to measure the frequency of an unknown signal by comparing it to that of an known frequency. By counting the number of horizontal and vertical nodes, complex ratios like 4:5 and 11:9 are easily recognized and the unknown frequency easily calculated.
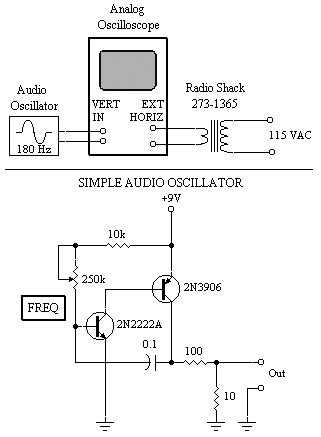
To have fun with Lissajous graphics, all you need is a sine-wave oscillator, a 12-volt power transformer, and an analog oscilloscope. That's it! Here's the setup, including the schematic for a very simple audio generator.



Comments