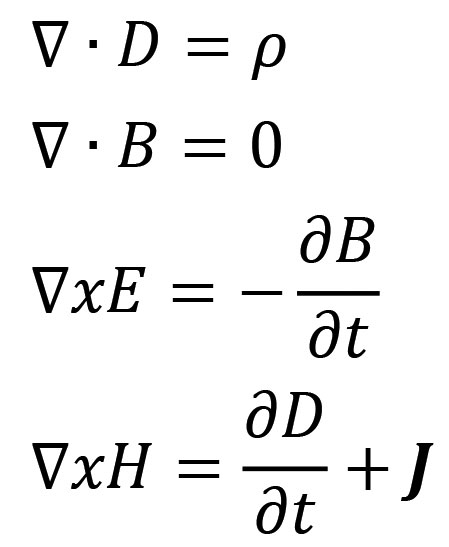When the concept of electromagnetic waves was first proposed around 1864, it was met with great skepticism. As a result, the idea languished for a long time. This is understandable since the foundations of the theory were complex and the conceptual ideas were at odds with physical thinking. It took several decades for a handful of dedicated persons — infatuated with the mysteries of electricity and magnetism — to finally put the theory on a solid footing.
In this article, we’ll take a look back at this period that launched the serious study of radio waves. We’ll examine the contribution of James Clerk Maxwell, the man most responsible for the concept. Next, we’ll look at the work of several notable scientists who came after Maxwell, and see how they confirmed the existence of radio waves.
We have a seemingly unlimited electromagnetic spectrum consisting of radio waves, microwaves, visible light, ultraviolet, x-rays, and gamma rays. How we came to discover and comprehend these astonishing waves is a captivating story. In what follows, we’ll look back at the historical underpinnings of electromagnetic waves — and we’ll do so without invoking theoretical derivations. But first, let’s examine what we mean when we talk about such waves.
Conceptually, an electromagnetic wave can be generated as shown in Figure 1. A more comprehensive picture of how electromagnetic waves are formed and their analogy to gravitational waves can be found at the URL noted in Reference 1.
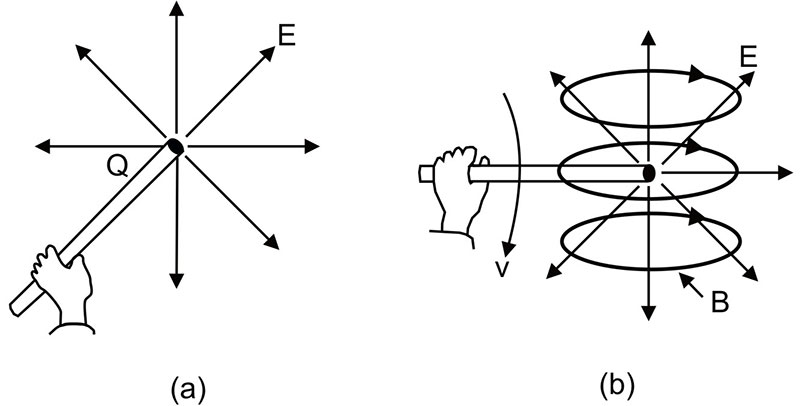
Figure 1. Assume that you have a stick with a certain amount of charge Q (a). When you hold the stick stationary, the charge is surrounded by an electric field E but no magnetic field (b). The same charge in motion creates a magnetic field B as well. If the stick is shaken up and down at frequency f, a small portion of the field escapes to propagate away as an electromagnetic wave at the same frequency.
Electromagnetic waves consist of both electric and magnetic field waves. These waves oscillate in perpendicular planes with respect to each other, and are in phase. A simple picture of a transverse electromagnetic wave propagating through space is shown in Figure 2.

Figure 2. Electromagnetic waves are formed when an oscillating charged particle creates ripples in its electric field and thereby also creates a magnetic field. A typical wave is shown here: an electric field coupled to a magnetic field. The fields of the wave are perpendicular to each other and to the direction of propagation of the wave.
The creation of an electromagnetic wave begins with an oscillating charged particle, which creates oscillating electric and magnetic fields. When accelerating — as part of the oscillatory motion — the charged particle radiates energy creating ripples (or oscillations) in its electric field, and also produces a magnetic field.
Once in motion, the electric and magnetic fields created by the charged particle are self-perpetuating — time-dependent changes in one field (electric or magnetic) produce the other. This means that an electric field that oscillates as a function of time will produce a magnetic field, and a magnetic field that changes as a function of time will produce an electric field. Consequently, both electric and magnetic fields in an electromagnetic wave will fluctuate in time, one causing the other to change.
If the charge’s frequency of oscillation is f, then it produces an electromagnetic wave with frequency f. The wavelength λ of this wave is given by λ = c/f where c is the speed of light. Electromagnetic waves transport energy through space. This energy can be delivered to charged particles a large distance away from the source.
The Strange Path to Maxwell’s Electromagnetic Theory
According to many science books, James Clerk Maxwell (Figure 3) is the person most responsible for providing the theoretical foundation for electromagnetic waves. What the books don’t tell you is that at the time of Maxwell’s death in 1879, his theory — which bolsters so much of our present technological world — was not yet on firm footing.

Figure 3. James Clerk Maxwell was a Scottish mathematical physicist, who formulated the classical theory of electromagnetic radiation, bringing together for the first time electricity, magnetism, and light as manifestations of the same phenomenon. He was one of the most influential scientists of the nineteenth century.
Science teachers tell us that the basic rules by which light and indeed all electromagnetic waves behave — such as electric fields and magnetism interactions — can be reduced to four elegant equations. Today, these equations — known as Maxwell’s equations — are found in just about every introductory engineering and physics textbook. It is little known [Reference 2] that Maxwell did not write these equations; although, he was mainly responsible for the theory behind them.
Let’s look back at the early development of electromagnetic theory. In later sections, we’ll look at events that occurred after Maxwell’s death.
Events Leading Up to Maxwell’s Electromagnetic Theory
Most historians agree that developments related to electromagnetic theory began in 1800 when physicist Alessandro Volta announced the invention of a battery, which allowed experimenters to work with a stable supply of direct current. Some years later, the first physical evidence of a link between electricity and magnetism was obtained by Hans Christian Oersted by demonstrating that the needle of a compass would shift when it was moved close to a wire carrying direct current.
Soon thereafter, Andrè-Marie Ampère showed that a mutual attraction or repulsion occurred between two parallel current-carrying wires depending on the relative direction of the currents. Then, around 1831, Michael Faraday showed that a magnet could affect electricity when he demonstrated that pulling a magnet through a coil of wire would produce a current.
These events were that were not understood in a systematic or complete way. They were indeed very perplexing. How could a current-carrying wire reach out and shift a compass needle? And, how could a moving magnet cause a current to flow in a wire?
Certainly, the natural philosophers and scientists conjectured on the manner in which electric and magnetic influences are transmitted through space. Most favored direct action-at-a-distance. Exploring a different approach, the foremost mathematician Karl Frederick Gauss, around 1855, considered the idea that electric actions propagate between the charges with finite velocity. However, he resolved not to publish his research until he could design a mechanism to achieve that transmission — which didn’t happen.
Faraday, a scientist-inventor, had also begun to challenge the orthodox view that electromagnetic phenomenon were the result of direct action-at-a-distance between electrical particles. Instead, he envisioned a mysterious invisible “electrotonic” state surrounding the magnet — what we would call a field. Changes in this electrotonic state, he said, are what caused electromagnetic phenomenon.
It is now known that in a deposition with the Royal Society of London known as “The Original Views,” Faraday considered the idea that electric and magnetic effects are “progressive and require finite time for their transmission.” Faraday did not find time to provide experimental evidence to support his views and hence wished the deposition, submitted in 1832, to remain unopened for 100 years. He stated that “ by depositing this paper in the care of the Royal Society, to take possession as it were of a certain date; and so have the right, if they are confirmed by experiments, to claim credit for the views at that date.”
However, historians do not attach much importance to this fascinating document and do not regard Faraday as the prime inventor of wave propagation. It was all well and good to prophesize about such phenomena, but shaping these ideas into a complete theory was far beyond his mathematical abilities. Nonetheless, Faraday’s dreams, once planted, were enough to stir the imagination of those who followed him.
This was the situation that Maxwell found during his formative years in the 1850s at the University of Cambridge in England. In the next section, we’ll set the foundation for his work in this field.
Maxwell Begins His Scientific Work
Maxwell was already an accomplished mathematician when he left Scotland for the University of Cambridge in 1850. He studied in Trinity, a college of Cambridge, under the tutelage of William Hopkins who was known for turning out mathematical geniuses.
After a brief interlude working on pure mathematics, his attention turned to physical problems such as electric and magnetic fields, the kinetic theory of gases, the nature of Saturn’s rings, and color vision. In his first attempt at electromagnetic theory, Maxwell wrote a paper in 1855 called “On Faraday’s Lines Of Force,” showing how the equations that describe incompressible fluid flow could analogously be used to solve problems with constant electric or magnetic fields.
Unfortunately, his work was disrupted by many difficulties. He was forced to leave his first teaching position at Marischal College in Scotland because of a college merger and nearly died from complications of smallpox. Finally, he ended up as a professor at King’s College, London.
Maxwell’s time at King’s was — by most accounts — the most productive of his career. This period of his life would see him produce the world’s first light-fast color photograph, develop his ideas on the viscosity of gases, and propose a system of defining physical quantities — now known as dimensional analysis.
Maxwell would often attend lectures at the Royal Institution, where he regularly came in contact with Faraday. The relationship between the two men was not close; partly because Faraday was 40 years’ Maxwell’s senior and showed signs of age. They nevertheless maintained a strong respect for each other’s work.
It was at this period in his life that Maxwell made significant theoretical advances. He examined the nature of both electric and magnetic fields in his two-part paper “On Physical Lines Of Force,” published in 1861. Therein he provided a conceptual model for electromagnetic induction consisting of tiny spinning cells of magnetic flux. Each cell is surrounded by small particles of some form that helped carry spin away from one cell to another.
Although he eventually discarded this concept, he found that this picture helped him describe a variety of electromagnetic phenomena. Perhaps, most importantly, it helped lay the basis of a radical new physical concept known as displacement current.
Displacement current is a difficult concept since it is not really a current. Normal conduction current found in wires consists of moving charges. Displacement current is a way of describing how the change in electric fields passing through a given area give rise to a magnetic field, just as a conduction current would do.
An ordinary capacitor holds within it one of the most striking examples of displacement current. Consider a parallel plate capacitor in an electric circuit with empty space between the plates as shown in Figure 4. If the capacitor is charging, that causes charge buildup on the plates and an increasing electric field Ε between the plates. This changing electric field causes a changing magnetic field B which is related to the so-called displacement current ID = IC. No conduction cur rent actually flows between the plates.
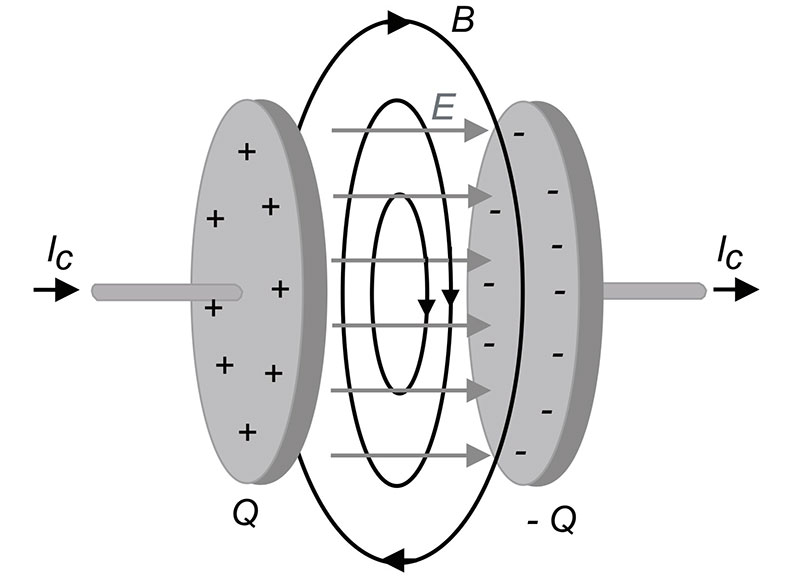
Figure 4. This is a parallel plate capacitor with empty space between the plates assumed to be in a charging circuit. Because of the charging, there is a changing electric field Ε between the plates, and consequently a displacement current ID (not shown) producing a magnetic field B. The displacement current ID has the same value as the conduction current IC that flows in the wires due to charge movement.
However, Maxwell’s displacement current is more fundamental than this example shows. It can arise in any medium including regions where electrons are available or not. And, just like a conduction current, it gives rise to a magnetic field.
Maxwell’s new concept provided the necessary bridge to link measureable circuit properties such as permittivity and permeability of free space. He somehow realized that these constants can be combined to determine how fast an electromagnetic wave travels in space.
Maxwell relied on others whose experiments on capacitors and inductors had determined their values very precisely. Using these numbers, Maxwell was able to calculate the speed of an electromagnetic wave in space. Amazingly, when he compared his value to the existing values of the speed of light, he concluded from their closeness that light must be an electromagnetic wave.
Maxwell Predicts Electromagnetic Waves
In 1864 when he was 33, Maxwell presented a paper “Dynamical Theory Of The Electromagnetic Field,” where he theorized that an electromagnetic disturbance travels in free space with the velocity of light. He also conjectured that light is a transverse electromagnetic wave even though this fact was somewhat hidden in the set of equations he proposed. Most importantly, he described how electricity and magnetism are inexorably linked in a moving electromagnetic wave.
When Maxwell introduced his theory at a presentation to the Royal Society, the audience was mystified. Maxwell had shown a fundamental shift in his approach. Instead of building imaginary physical models, he tried to discern scientific truth from well established mathematical relations known as the laws of dynamics.
To the audience, a difficult physical model would be bad enough, but a theory based on no model at all was beyond their comprehension! Their perplexed state is understandable since Maxwell’s paper was long, hard to grasp quickly, and the mathematics was difficult to follow.
It described how various variables interacted and how they moved in space and time. More confusingly, it used the concepts of vectors to represent electric and magnetic field intensities and flux densities. Few people of the time understood vectors. For newcomers, it was especially difficult since each vector came as triple — one equation for each of the three dimensions.
Maxwell also employed a counter-intuitive variable he invented known as electromagnetic momentum — known today as magnetic vector potential — from which he calculated the electric and magnetic fields.
All told, Maxwell introduced 20 equations involving 20 variables. For those interested in studying all of them in detail, see Reference 3. Through these equations, Maxwell essentially unified the work of Oersted, Gauss, Ampère, Faraday, and others while adding his own radical concept of displacement current. Today, this theory is the foundation of our modern understanding of electromagnetism.
All of this work was met with extreme skepticism even from his closest colleagues. Sir William Thompson — later Lord Kelvin — was one of the loudest skeptics. He simply did not believe a displacement current could exist. Our intuition would agree with him.
It was one thing to think of a displacement current in a material filled with atoms. It was quite another to imagine it forming in the emptiness of space! Without a model to describe this displacement current — one that works without moving charges — it was not clear how such a current could arise. This whole concept was very repulsive to the scientists of the time.
Today, we readily accept radical theories. We accept black holes, gravitational waves, the Higgs field, quantum entanglement, and other theories that defy everyday intuition. We do so as long as the mathematical foundations are sound and can be verified to some extent.
Because of all the complexity surrounding the debut of Maxwell’s work, it was not met with enthusiasm. One could more accurately say that practically no one was interested!
Maxwell Publishes the “Treatise”
Maxwell had put his new electromagnetic theory on full public display, but it was ignored by most. It would be some time before it would be appreciated. No one, perhaps not even Maxwell, understood the full significance of his work.
Maxwell had thrived on a full assortment of work during his five years in London, but he still yearned for country life. So, he decided to resign his chair so that he and his wife, Katherine could take up a settled life in his old Glenlair House in Galloway in 1865.
The years Maxwell spent at Glenlair were in no sense a time of retirement. His work on electromagnetism was far from finished. He wanted to write a substantial book; one that would bring much-needed order to the subject, help newcomers, and establish a solid base for future work.
n 1873, Maxwell published his book “Treatise On Electricity And Magnetism,” where he expounded further on many of his ideas. Still in print, it is one of the most renowned books in physics. However, the “field” concept in the book was alien to physicists and his mathematics seemed like a backward step in the art.
His fields obeyed partial differential equations which were far more difficult to handle than current Newtonian force laws. Without adequate mathematical interpretation, his theory of electromagnetism hung like a museum painting on the wall, admired by some but out of reach.
Maxwell died in 1879 at age 48 with Katherine and a friend at his bedside. He was a lone pioneer as was Faraday before him. Almost nobody understood his “Treatise” during his lifetime. Not until the following generation — led by a small band of individuals known as the “Maxwellians” (Reference 4) — did anyone truly understand what he was trying to say. Oliver Heaviside was one of these.
Heaviside Arrives On the Scene
Oliver Heaviside (Figure 5) was once described by a friend as a “first rate oddity.” He was actually the forgotten genius of the Victorian age. He was the youngest of four sons, born in 1850 to a poor but respectable family in London. At the age of eight, scarlet fever left him partially deaf making it hard to play with other boys. Subsequently, he relied on his own resources and developed a stubborn independence that he held to the day he died.

Figure 5. Oliver Heaviside was a reclusive mathematical genius who spent most of his life on the fringe of the science establishment. In spite of this, he did more than anyone else to shape Maxwell’s theory and put Maxwell’s equations into their present form.
He did well at school but was denied a university education because it was beyond the family’s resources. Heaviside taught himself science and mathematics — learning from the journals and books of the day.
Through the influence of his uncle, Charles Wheatstone (of bridge fame), he got his first and only job at the age of 18 as a telegraph operator on the Anglo-Danish cable running from Newcastle to Denmark. In this capacity, he had the opportunity to learn firsthand about the most advanced and scientifically interesting branch of electrical engineering.
Telegraph equipment of the time used visual cues, so his mild deafness did not play a role. He loved communicating in Morse code, but fixing faults in the cable system was what he really enjoyed. Telegraphers, being the elite of the group, were free to experiment with many electrical components like bridges and condensers. To be sure, they had to know these components well to keep the traffic moving.
Heaviside eventually became the star troubleshooter, enjoying each problem and the puzzling effects of electricity that often baffled his colleagues. In his free time, he continued his studies into electricity and mathematics, and even began writing scientific papers.
One day, he came across a copy of Maxwell’s “Treatise” and was immediately impressed. Although much of the mathematics was far above his head, he became determined to master it. By this time, Heaviside had already decided to devote all his attention to electricity. He had left his telegraphers job and returned to his parent’s home where he began pushing back the frontiers of electrical knowledge.
It was Heaviside working at home alone that developed Maxwell’s equations in their present form. Plowing through the complicated vector calculus, he happened upon a way to reformulate Maxwell’s 20 confusing equations into the four we use today, shown in Figure 6.
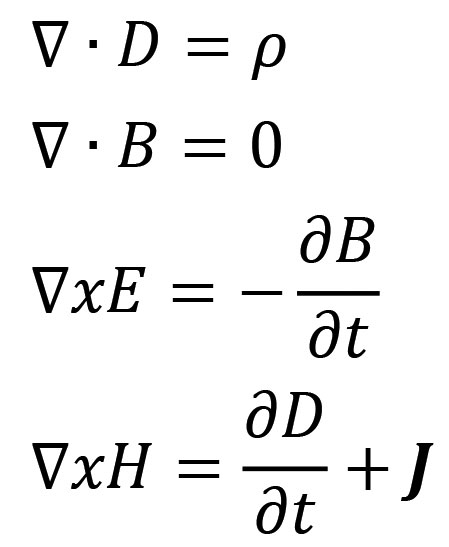
Figure 6. Around 1884, Oliver Heaviside began writing the 20 fundamental equations of Maxwell’s “Treatise On Electricity And Magnetism” into the new and more compact form shown here. They have become the standard that today defines the relationship between electricity and magnetism and the wave nature of electromagnetic radiation. Shown here is the differential form of Maxwell’s equations, but other forms exist such as the integral form. Here, Ε and B are the electric and magnetic fields respectively, ρ is the electric charge density, and J is the current density. There are two other fields — the displacement field D and the magnetic field strength H — related to Ε and B by constants that reflect the nature of the medium that the fields pass through.The displacement field was the key contribution of Maxwell. The last equation describes how both changing electric fields and current produce magnetic fields. The symbol ∇ is a vector differential operator, commonly called Del or nabla that compactly expresses the calculus that involves directionality of the three x, y, and z components.
Heaviside said the key was removing the strange magnetic vector potential. According to Heaviside, “I never made any progress until I threw all the potentials overboard.” Heaviside’s formulation placed the electric and magnetic fields at the forefront.
While Heaviside’s formulation exposed the beautiful symmetry of Maxwell’s equations, they also exposed a mystery. Electric charges have lines of electric field around them emanating from the charge. However, the magnetic field lines — as we know them — have no source and appear only in continuous loops, with no start or end.
Heaviside was troubled by this and added a term to the equations to represent magnet charge assuming it had not been discovered yet. In fact, magnetic monopoles still haven’t been found, although they have been predicted by some particle theories. Yet, the notion of magnetic current, composed of fictitious moving monopoles, persists and is sometimes used as an aid in solving some problems.
Heaviside was often asked why we don’t call these equations Heaviside’s equations. He said that he believed that Maxwell — with good reason — “would have admitted to the necessity of the changes when pointed out to him.” Hence, he felt they should be called Maxwell’s equations.
Refining a mathematical theory was one thing, but finding experimental evidence to support it was something else. With the help of two other Maxwellians and a little known German researcher, Heinrich Hertz, the fog began to lift.
Other Maxwellians Arrive On the Scene
Up to 1888, Heaviside was doing the same things: reading journals, writing papers that were seldom read, and rarely travelling from his home. One day, he happened upon a report by Oliver Joseph Lodge (Figure 7), professor of physics at University College in Liverpool, wherein he was mentioned for his work on Maxwell’s theory.
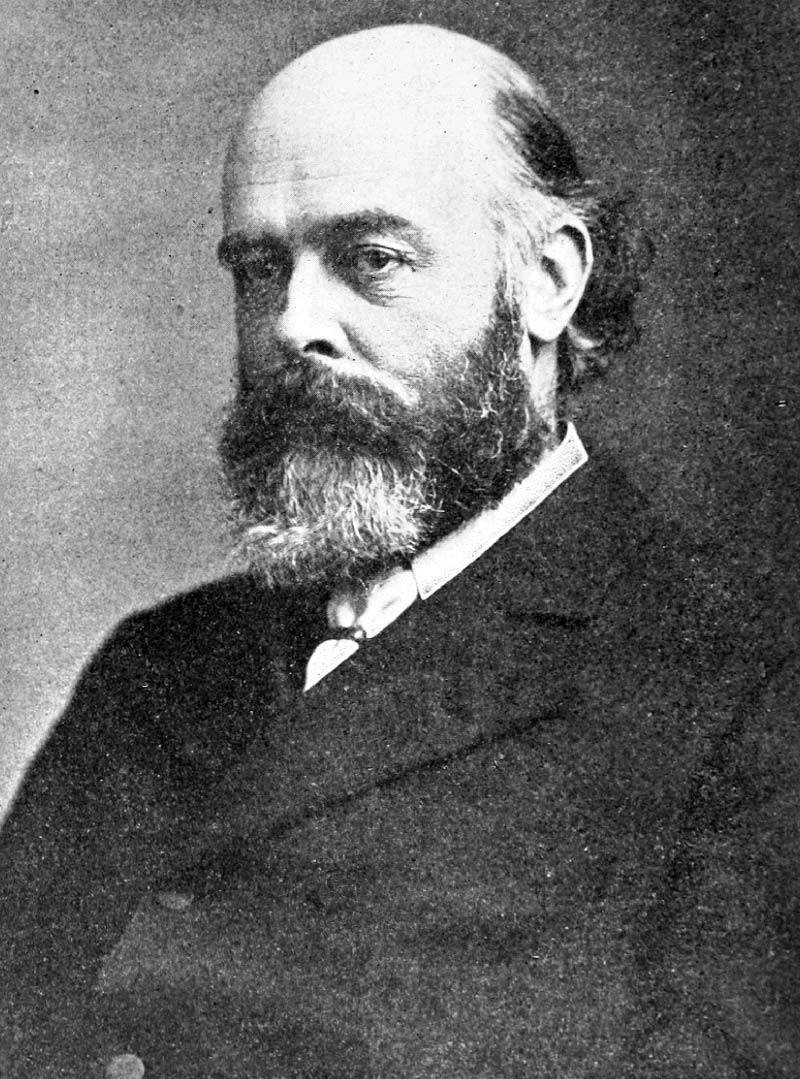
Figure 7. Oliver Joseph Lodge was a British physicist who studied electromagnetic radia tion. He made a particularly strong mark in the field of wireless telegraphy. In 1894, he perfected the “coherer:” an electrical device used to detect radio waves. Lodge’s version of the coherer greatly improved the detection of radio waves.
Overjoyed to find a kindred spirit, Heaviside promptly wrote to Lodge and found he had another admirer, Lodge’s friend George Francis Fitzgerald (Figure 8), a professor of experimental philosophy at Trinity College in Dublin.
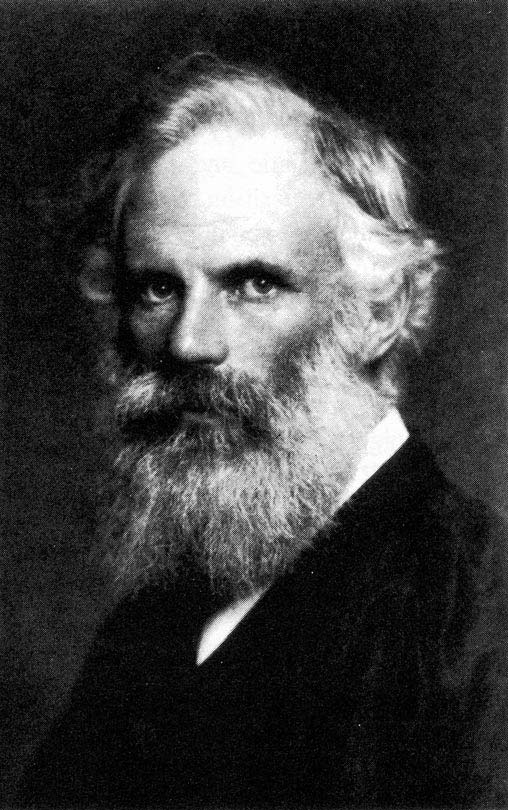
Figure 8. George Francis Fitzgerald was an Irish professor of physics at Trinity College in Dublin, Ireland. He is known for his work in electromagnetic theory and for the Lorentz–Fitzgerald contraction, which became an integral part of Einstein’s special theory of relativity.
It turned out that Lodge and Fitzgerald were captivated by Maxwell’s work and were trying — with mutual support — to carry it forward, largely through the exchange of letters. Fitzgerald was a brilliant theoretician but a bit lazy when it came to experimental work. However, he was one of the very few people who read and learned the “Treatise” in detail.
Lodge, on the other hand, was more comfortable using models rather than equations and enjoyed experimental work. Heaviside’s bond with them was immediate, and they began collaborating in the hope of advancing the understanding of Maxwell’s theory.
Lodge and Fitzgerald were particularly interested in finding experimental evidence to support the idea that light is an electromagnetic wave. They didn’t have much success in this endeavor initially. One day, Lodge was experimenting with a lightning protection system in preparation for a talk to the Society of Arts.
He endeavored to simulate lightning by discharging Leyden jars across the wires. Sparks appeared between the ends of the wires. This was expected, but soon he found that by varying the wire lengths he could make very large sparks or weaker ones. He realized immediately that he was seeing an electromagnetic wave in resonance. With enough power, he claimed to actually see the ionized standing wave around the wire.
Lodge planned on reporting his astonishing results when he returned back from a vacation in the Alps. For the trip, he took along some unread journals. While on the train leaving from Liverpool, he was crestfallen to read about similar work in the July issue of Annalen der Physik und Chemie by Heinrich Hertz, the German researcher. Hertz (Figure 9) had produced and detected waves not only along wires, but in free space.

Figure 9. Heinrich Hertz was a brilliant German physicist and experimentalist who demonstrated that the electromagnetic waves predicted by James Clerk Maxwell actually exist. In November 1886, Hertz became the first person to transmit and receive controlled radio waves.
More incredibly, he had measured the speed of the waves and showed that they could be refracted, reflected, and polarized the same as light. Lodge, of course, was severely disappointed that he was outdone, but this was more than overshadowed later on by the newfound admiration of the German’s work.
Experimental Evidence for Radio Waves
Hertz’s experimental work began in the 1880s at the Technische Hochschule in Karlsruhe, Germany. At this time, there were various electromagnetic theories, including Maxwell’s. Hertz was encouraged by his mentor Hermann von Helmholtz, to differentiate the theories. Hertz tried an experiment to detect displacement currents, but he found nothing.
Several years later, in the course of setting up an experiment for a classroom demonstration, he noticed while discharging a condenser through a loop, that an identical loop some distance away developed arcs. He instantly recognized a resonance condition and suspected electromagnetic waves. Now inspired, Hertz began using such loops to detect unseen radio waves, and verified most of the properties of electromagnetic waves. A photo of his lab is shown in Figure 10.

Figure 10. Hertz took this photo of his lab. It shows the coil that he used (left) and the antenna — a dipole resonator with spark gap that he used to detect electromagnetic radiation.
In one interesting test, Hertz transmitted radio waves toward a grid of parallel wires and verified that they would pass through or be reflected depending on the angle of the grid. This showed that electromagnetic waves were transverse waves and oscillating, as light does, perpendicular to the direction of propagation. In another experiment using a zinc sheet as a reflector, he moved the detector around and found places of sparking and others of no sparking. This was evidence of a standing wave formed by a travelling wave combined with its reflection from the screen.
Hertz’s findings attracted little attention in Germany. However, across the channel, the Maxwellians showered him with praise, welcomed him into their ranks, and began promoting his work. Lodge, for example, made a replica of Hertz’s apparatus which he demonstrated before the British Association and other groups. Heaviside was so elated, he wrote Hertz thanking him for providing the experimental proof, saying he had given “the death blow” to the action-at-a-distance theories.
Hertz, Lodge, Fitzgerald, and Heaviside became a close and mutually supportive group. Through the efforts of these four very different persons — joined in a common cause — they brought Maxwell’s theory out of the shadows and into the light.
Epilog
The Maxwellians had built up a solid friendship through their correspondence, and succeeded in revising and transforming Maxwell’s theory in many ways. They gave us the equations we currently use today and they were the ones who gave us the confirming evidence that light is an electromagnetic wave. Most importantly, they got Maxwell’s theory accepted by the scientific community.
Unfortunately, their heyday lasted for only a few years, from 1888 to 1894. Tragically, Hertz died in 1894 from a rare bone disease at the early age of 36. We’ll never know what other wonderful things he could have accomplished.
Fitzgerald also died at the young age of 49. In addition to his work on Maxwell’s theory, he is remembered today as one of the proposers of a theory on the relativity of space with speed, now known as the Lorentz–Fitzgerald contraction. This later became a crucial part of Einstein’s special theory of relativity.
Lodge lived until 1940 and continued his work in many fields including radio. In 1894, he perfected a “coherer:” an electrical device to detect radio waves.
Heaviside corresponded with other scientists and continued publishing until he died in 1926. His other achievements include using complex numbers to study electrical circuits, inventing the step function, and developing mathematical techniques for solving differential equations. He is perhaps best known for his prediction that earth’s atmosphere had an ionized reflective layer capable of bouncing radio signals back to earth, such that the radio signals followed earth’s curvature — now known as the Kennelly-Heaviside layer in his honor.
Maxwell’s theory of the electromagnetic field had a momentous effect on science, but theories seldom spring from the minds of their creators fully completed. As so often happens, the next generation of scientists has to refine and codify it — a process that can take years. So it was with Maxwell’s theory.
Albert Einstein once said: “The special theory of relativity owes its origins to Maxwell’s equations of the electromagnetic field. Since Maxwell’s time, physical reality has been thought of as represented by continuous fields, and not capable of any mechanical interpretation. This change in the conception of reality is the most profound and the most fruitful that physics has experienced since the time of Newton.”
Maxwell’s achievement was honored by two IEEE Milestone ceremonies in 2009: one in Glenlair House; and the other at King’s College. The plaques inform visitors that between 1860 and 1871, Maxwell developed his unified theory of electricity, magnetism, and light, summarized in the equations that bear his name. One of the plaques (engraved with the famous equations) is shown in Figure 11.

Figure 11. Two IEEE Milestone ceremonies were held in Glenlair House and at King’s College in 2009 to commemorate the publication of Maxwell’s equations. This is one of the plaques that inform visitors of his unified theory of electricity, magnetism, and light, summed up in the equations that bear his name.
Some prescient words from Heaviside seem appropriate at this point. “The great gap between Hertzian waves and waves of light has not yet been bridged, but I do not doubt that it will be done by the discovery of improved methods of generating and observing very short waves.” Very prophetic words indeed!
In closing, I would like to dedicate this article to my former student and longtime friend, Dr. Steven E. Reyer, who recently passed away unexpectedly. His presence will be truly missed. NV
REFERENCES
[1] www.tapir.caltech.edu/~teviet/Waves/emfield.html
[2] James C. Rautio, “The Long Road To Maxwell’s Equations,” IEEE Spectrum, Dec. 2014.
[3] T.K. Sarkar, et. al, “History Of Wireless,” Wiley IEEE Press 2006.
[4] Bruce J. Hunt, “The Maxwellians,” Cornell University 2005.